Graph Traversal - BFS

BFS (Breadth First Search)
BFS traversal of a graph produces a spanning tree as final result. Spanning Tree is a graph without loops. We use Queue data structure with maximum size of total number of vertices in the graph to implement BFS traversal.

Note:BFS Follows level order traversals of a given tree in its conclusion  


We use the following steps to implement BFS traversal...

Step 1 - Define a Queue of size total number of vertices in the graph.
Step 2 - Select any vertex as starting point for traversal. Visit that vertex and insert it into the Queue.
Step 3 - Visit all the non-visited adjacent vertices of the vertex which is at front of the Queue and insert them into the Queue.
Step 4 - When there is no new vertex to be visited from the vertex which is at front of the Queue then delete that vertex.
Step 5 - Repeat steps 3 and 4 until queue becomes empty.
Step 6 - When queue becomes empty, then produce final spanning tree by removing unused edges from the graph

Algorithm of BFS :

1. set status of all vertex=1
2. insert the starting vertex in queue and set its status=2
3. while(queue is not empty)
4.     remove front vertex in queue and set its status=3
5.     if(status of neighbors = 1)
6.     then insert neighbors in queue and set its status=2
7. end of while
8. exit

Example

Introduction To Graphs

Graph is a non-linear data structure. It contains a set of points known as nodes (or vertices) and a set of links known as edges (or Arcs). Here edges are used to connect the vertices. A graph is defined as follows...

Graph is a collection of vertices and arcs in which vertices are connected with arcs

                              OR
Graph is a collection of nodes and edges in which nodes are connected with edges

Generally, a graph G is represented as G = ( V , E )
where V is set of vertices
           E is set of edges.

Example

The following is a graph with 5 vertices and 7 edges.
This graph G can be defined as G = ( V , E )
Where V = {A,B,C,D,E} and E = {(A,B),(A,C)(A,D),(B,D),(C,D),(B,E),(E,D)}.

Graph Terminology

Vertex

Individual data element of a graph is called as Vertex. Vertex is also known as node. In above example graph, A, B, C, D & E are known as vertices.

Edge
An edge is a connecting link between two vertices. Edge is also known as Arc. An edge is represented as (startingVertex, endingVertex).For example, in above graph the link between vertices A and B is represented as (A,B). In above example graph, there are 7 edges (i.e., (A,B), (A,C), (A,D), (B,D), (B,E), (C,D), (D,E)).

Edges are three types.

Undirected Edge - An undirected egde is a bidirectional edge. If there is undirected edge between vertices A and B then edge (A , B) is equal to edge (B , A).

Directed Edge - A directed egde is a unidirectional edge. If there is directed edge between vertices A and B then edge (A , B) is not equal to edge (B , A).

Weighted Edge - A weighted egde is a edge with value (cost) on it.

Degree
Total number of edges connected to a vertex is said to be degree of that vertex.

Indegree
Total number of incoming edges connected to a vertex is said to be indegree of that vertex.

Outdegree

Total number of outgoing edges connected to a vertex is said to be outdegree of that vertex.

Self-loop
Edge (undirected or directed) is a self-loop if its two endpoints coincide with each other.

Simple Graph
A graph is said to be simple if there are no parallel and self-loop edges.

Path
A path is a sequence of alternate vertices and edges that starts at a vertex and ends at other vertex such that each edge is incident to its predecessor and successor vertex.

Types of graphs

Graph Traversal - DFS

Graph traversal is a technique used for a searching vertex in a graph. The graph traversal is also used to decide the order of vertices is visited in the search process. A graph traversal finds the edges to be used in the search process without creating loops. That means using graph traversal we visit all the vertices of the graph without getting into looping path.

There are two graph traversal techniques and they are as follows...

DFS (Depth First Search)
BFS (Breadth First Search)

DFS (Depth First Search)
DFS traversal of a graph produces a spanning tree as final result. Spanning Tree is a graph without loops. We use Stack data structure with maximum size of total number of vertices in the graph to implement DFS traversal.

Note:DFS Follows level order Preorder traversals of a given tree in its conclusion  

We use the following steps to implement DFS traversal...

Step 1 - Define a Stack of size total number of vertices in the graph.
Step 2 - Select any vertex as starting point for traversal. Visit that vertex and push it on to the Stack.
Step 3 - Visit any one of the non-visited adjacent vertices of a vertex which is at the top of stack and push it on to the stack.
Step 4 - Repeat step 3 until there is no new vertex to be visited from the vertex which is at the top of the stack.
Step 5 - When there is no new vertex to visit then use back tracking and pop one vertex from the stack.
Step 6 - Repeat steps 3, 4 and 5 until stack becomes Empty.
Step 7 - When stack becomes Empty, then produce final spanning tree by removing unused edges from the graph

Algorithm of DFS :

1. set status of all vertex=1
2. push the starting vertex onto stack and set its status=2
3. while(stack is not empty)
4.     pop the top vertex of stack and set its status=3
5.     if(status of neighbors = 1)
6.     then push onto stack and set its status=2
7. end of while
8. exit

Example:

Graph Representations

Graph data structure is represented using following representations...

Adjacency Matrix

Incidence Matrix

Adjacency List

Adjacency Matrix

In this representation, the graph is represented using a matrix of size total number of vertices by a total number of vertices. That means a graph with 4 vertices is represented using a matrix of size 4X4. In this matrix, both rows and columns represent vertices. This matrix is filled with either 1 or 0. Here, 1 represents that there is an edge from row vertex to column vertex and 0 represents that there is no edge from row vertex to column vertex.

For example, consider the following undirected graph representation

Directed graph representation...

Incidence Matrix

In this representation, the graph is represented using a matrix of size total number of vertices by a total number of edges. That means graph with 4 vertices and 6 edges is represented using a matrix of size 4X6. In this matrix, rows represent vertices and columns represents edges. This matrix is filled with 0 or 1 or -1. Here, 0 represents that the row edge is not connected to column vertex, 1 represents that the row edge is connected as the outgoing edge to column vertex and -1 represents that the row edge is connected as the incoming edge to column vertex.

For example, consider the following directed graph representation

Adjacency List
In this representation, every vertex of a graph contains list of its adjacent vertices.


For example, consider the following directed graph representation implemented using linked list.

This representation can also be implemented using an array as follows

Threaded Binary Tree

       Inorder traversal of a Binary tree can either be done using recursion or with the use of a auxiliary stack. The idea of threaded binary trees is to make inorder traversal faster and do it without stack and without recursion. A binary tree is made threaded by making all right child pointers that would normally be NULL point to the inorder successor of the node (if it exists).

In memory representation of threaded binary tree node is represented by

LThread

Data

RThread

Each node of any binary tree stores the three fields. The left field stores the left thread value and the right field stores the right thread value. The middle field contains the actual value of the node i.e.., data.

There are two types of threaded binary trees.

Single Threaded: Where a NULL right pointers is made to point to the inorder successor (if successor exists)

        In one way inorder threading the right child of the node would point to the next node in the sequence of the inorder traversal, such a threading tree is called “Right in threaded binary tree”. Also, the left child of the node would point to the previous node in the sequence of inorder traversal, this type of tree is called as “Left in threaded binary tree”. In case both the children of the nodes point to other nodes then such a tree is called “Fully threaded binary tree”.

         Figure(1) describes the working of right in threaded binary tree in which one can see that the right child of the node points to the node in the sequence of the inorder traversal method.

Example:

        The inorder traversal shown in fig(1) will be as D B H E A F C G. Two dangling pointers are shown to point a header node as

Rchild of D is made to point to B

Rchild of E is made to point to A

Rchild of F is made to point to C
Rchild of H is made to point to E

Fig (2) describes the working of “left in threaded binary tree”.

In this case the left child of node points to the previous node in the sequence of inorder traversal. As shown in fig (2), thread of E points to B. Here B is the predecessor of E in inorder traversal. Hence, the pointer points to B. In this type of tree the pointers pointing to other nodes are as follows.

Lchild of H is made to point to B

Lchild of F is made to point to A
Lchild of G is made to point to C

Double Threaded: Where both left and right NULL pointers are made to point to inorder predecessor and inorder successor respectively. The predecessor threads are useful for reverse inorder traversal and postorder traversal.

Fig illustrates the operation of fully threaded binary tree

Right and left children are used for pointing to the nodes in inorder traversal method.

Rchild of A is made to point to C

Lchild of A is made to point to B

Rchild of B is made to point to A

Lchild of B is made to point to D

Rchild of D is made to point to B

Lchild of D is made to point to DUMMY NODE

Lchild of C is made to point to A

Rchild of C is made to point to E

Rchild of E is made to point to DUMMY NODE

Lchild of E is made to point to C

Binary Search Tress - Insertion & Deletion

Binary Search Tree is a node-based binary tree data structure which has the following properties:

·       The left subtree of a node contains only nodes with keys lesser than the node’s key.

·       The right subtree of a node contains only nodes with keys greater than the node’s key.

·    The left and right subtree each must also be a binary search tree.

Basic Operations: Following are the basic operations of a tree 

Search − Searches an element in a tree.

Insert − Inserts an element in a tree.

Pre-order Traversal − Traverses a tree in a pre-order manner.

In-order Traversal − Traverses a tree in an in-order manner.

Post-order Traversal − Traverses a tree in a post-order manner.

Binary Search Tree (Search and Insertion)

Binary Search Tree, is a node-based binary tree data structure which has the following properties:

• The left subtree of a node contains only nodes with keys lesser than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• The left and right subtree each must also be a binary search tree.
• There must be no duplicate nodes.

Search Operation

        Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.

Insert Operation

      Whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data.

• Binary Search Tress - Insertion

Binary Search Tress -  Deletion :Deletion of a node is performed as follows,

Deleting node has no child, therefore just delete the node(made to point NULL)

Deleting node has 1 child, swap the key with the child and delete the child.

Deleting node has 2 children, in this case swap the key with inorder successor of the deleting node. It should be noted, inorder successor will be the minimum key in the right subtree (of the deleting node).

Trees

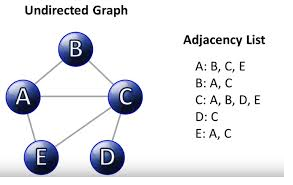
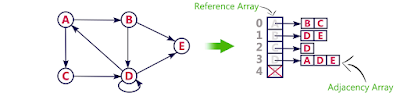
INTRODUCTION OF TREES:
         Trees are one of the most important data structures in computer science. Trees are very flexible, versatile and powerful data structures that can be used to represent data items possessing hierarchical relationship between the grandfather and his descendants and their descendants and so on.

        A tree is a non-linear data structure in which items are arranged in a sorted sequence. It is used to represent hierarchical relationship existing among several data items.

DEFINITION: 
Tree is a finite set of one or more data items(nodes)” such that
1.  There is a special data item called the root of the tree

2. The remaining data items are partitioned into number of mutually exclusively (i.e.., disjoint) subsets, each of which is itself a tree, and they are called “Subtrees”.

TREE TERMINOLOGY:

        There are number of terms associated with the trees which are    listed below-     

1.  Root

2.  Node

3.  Degree of a node

4.  Degree of a tree

5.  Terminal node

6.  Non-terminal node

7.  Siblings

8.  Level

9.  Edge

10.Path

11.Depth

12.Height

13.Forest

(1)  ROOT:-  It is specially designed data item in a tree. It is the first in the hierarchial arrangement of data items. In the above tree,
A is the root item.                                                                                    

(2) Node:- Each data item in a tree is called a node. It is the basic structure in a tree, it specifies the data information and links (branches) to other data items. There are 8 nodes in the above tree.

(3) Degree of a node:- In the above tree-

                        The degree of node A is 2

                        The degree of node C is 1

                        The degree of node B is 3

                        The degree of node H is 0

                      

(4) Degree of a tree:- It is the maximum degree of nodes in a given tree. In the above tree the node A has degree 3 and another node C is also having its degree 1. In all this, value is the maximum. So, the degree of the above tree is 3.

(5) Terminal node (or) leaf node (s);- A node with degree zero is called a terminal node (or) a leaf. In the above tree, there are 4 terminal nodes, they are D,F,G,H.

(6) Non-terminal node (or) internal node (s):-Any node (except the root node) whose degree is not zero is called non-terminal node. Non-terminal nodes are the intermediate nodes in traversing the given tree from its root node to the terminal nodes (leaves). There are 3 non-terminal nodes B, E,C.

(7) Siblings;- The children nodes of a given parent node are called “siblings”. They are also called brothers. In the above tree,
Ø B and C are siblings of parent node A.
Ø D,E,F are siblings of parent node B.

(8) LEVEL:- The entire tree structure is leveled in such a way that the root node is always at level 0. Then, its immediate children are at level 1 and their immediate children are at level 2 and so on upto the terminal nodes. In general, if a node is at level n, then its children will be at level n+1, in the 4 levels.

(9) EDGE:- It is a connecting line of two nodes. i.e.., the line drawn from one node to another node is called an edge.

(10) PATH:- It is a sequence of consecutive edges from the source node to the destination node. In the above tree, the path between A and H is given by the node pairs.

                        (A, B), (B, E) and (E,H)

(11) DEPTH:- It is the maximum level of any node in a given tree towards the root node is called  Depth 
In the above tree, the root node B has the Depth of 1 
the root node E has the Depth of 2  

(12) HEIGHT:-It is the maximum level of any node in a given tree towards the leaf node is called Height 
In the above tree, the root node B has the Height of 2 
the root node C has the Height of 1  

(13) FOREST:- It is a set of disjoint trees. In a given tree, if you remove its root node then it becomes a forest. In the above tree, there is forest with three trees.

BINARY TREES:-

        A binary tree is a finite set of data items which is either empty or consists of a single item called the root and two disjoint binary trees called the left subtree and right subtree.

A binary tree is a very important and the most commonly used non-linear data structure. In a binary tree the maximum degree of any node is atmost two. i.e.., there may be a zero degree node (usually an empty tree) or a one degree node and two degree node. Figure shows a binary tree consisting of 6 elements.

        In the above binary tree, A is the root of the tree. The left subtree consists of the tree with root B, and the right subtree consists of the tree with root C. Further B has its left subtree with root D 

        Similarly, C has its left subtree with root E and its right subtree with root F. In the next level, D has an empty left subtree. F has neither its left subtree nor right subtree 

FULL/STRICTLY BINARY TREES:-  If every non-terminal node in a binary tree consists of non-empty left subtree, then such a tree is called strictly binary tree.

NOTE: EVERY NODE MUST HAVE 2 CHILDREN EXCEPT THE LEAF NODE

COMPLETE/ PERFECT BINARY TREE:-  A binary tree with ‘n’ nodes and depth ‘d’ is a strictly binary tree all of  whose terminal nodes are at level ‘d’. In a complex binary tree, there is exactly one node at level 0, two nodes at level 1, and four nodes at level 2 and so on.

        If there are m nodes at level 1then a binary tree contains at most 2m nodes at level 1+1. A binary tree has exactly one node at the root level and has at most 2¹ nodes at level 1. Taking into consideration of this property, we can show further that a complete binary tree of depth d contains exactly 2¹ nodes at each level. The value 1 ranges from 0 to d. Figure shows a complete binary tree of depth 4.

NOTE: EVERY NODE MUST HAVE 2 CHILDREN IN ALL THE LEVELS AND AT EACH LEVEL THERE SHOULD BE 2 POWER LEVEL NODE ( I.E LEVEL 2 SHOULD HAVE 4 NODES )

INCOMPLETE/ALMOST BINARY TREE: every node must have two children in all the levels except in the last level  , fill the nodes from left to right 

TRAVERSING  IN  A  BINARY TREE (OR)

BINARY TREE APPLICATIONS:-

In tree creation we take 3 parameters node, left child and right child, so traversing of binary tree means traversing of node, left subtree and right subtree.

If root is denoted as N, left subtree as L and right subtree as R, then there will be six combinations of traversals.
Ø NRL
Ø NLR
Ø LNR
Ø LRN
Ø RNL
Ø RLN

But only three standard,   NLR (node-left-right) preorder

                                       LNR (left-node-right) in order

                                       LRN (left-right-node) post order

Preorder (NLR traversal)-

1.  Visit the root.

2.  Traverse the left subtree of root in preorder.

3.  Traverse the right subtree of root in preorder.

Inorder (LNR traversal)-

1.  Traverse the left subtree of root in inorder.

2.  Visit the root.

3.  Traverse the right subtree of root in inorder.

Postorder (LRN traversal)-

1.  Traversal the left subtree of root in postorder.

2.  Traverse the right subtree of root in postorder.

3.  Visit the root.

OPERATIONS  ON  BINARY TREES:-

        The basic operations to be performed on a binary are listed as follows-

1.  CREATE- It creates an empty binary tree.

2.  MAKE BINARY TREE- It creates a new binary tree having a single node with data field set to some value.

3.  EMPTY BINARY TREE- It returns true if the binary tree is empty otherwise it returns false.

4.  LEFT CHILD- It returns a pointer to the left child of the node. If the node has no left child it returns the null pointer.

5.  RIGHT CHILD- It returns a pointer to the right child of the node. If the node has no right child it returns the null pointer.

6.  FATHER- It returns a pointer to the father of the node. Otherwise returns the null pointer.

7.  BROTHER- It returns a pointer to the brother of the node. Otherwise returns the null pointer.

8.  DATA- It returns the contents of the node.

Apart from these primitive operations, other operations can be applied to the binary tree are –

Ø Tree traversal

Ø Insertion of nodes

Ø Deletion of nodes

Ø Searching for the node

Ø Copying the binary tree.

BINARY TREE REPRESENTATIONS-

                        There are two ways by which we can represent a binary tree.
(1)Linked representation of a binary  tree
(2)Array representation of a binary tree

(1)LINKED REPRESENTATION OF A BINARY TREE- The basic component to be represented in a binary tree is a node. The node consists of three fields such as

ü Data

ü Left child

ü Right child

The data field holds the value to be given. The left child is a link field which contains the address of its left node and the right child contains the address of the right node. Figure shows a structure of a node.

(2)Array representation of a binary tree

        An array can be used to store the nodes of a binary tree. The nodes stored in an array are accessible sequentially. In C, arrays start with index 0 to (maxsize-1). The maximum number of nodes is specified by MAXSIZE.

        The root node is always at index 0. Then in successive memory locations the left child and right child are stored. Consider a binary tree with only three nodes as shown. Let BT denote a binary tree.