Graph is a non-linear data structure. It contains a set of points known as nodes (or vertices) and a set of links known as edges (or Arcs). Here edges are used to connect the vertices. A graph is defined as follows...
Graph is a collection of vertices and arcs in which vertices are connected with arcs
OR
Graph is a collection of nodes and edges in which nodes are connected with edges
Generally, a graph G is represented as G = ( V , E )
where V is set of vertices
E is set of edges.
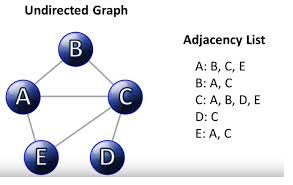
Example
The following is a graph with 5 vertices and 7 edges.
This graph G can be defined as G = ( V , E )
Where V = {A,B,C,D,E} and E = {(A,B),(A,C)(A,D),(B,D),(C,D),(B,E),(E,D)}.
Graph is a collection of vertices and arcs in which vertices are connected with arcs
OR
Graph is a collection of nodes and edges in which nodes are connected with edges
Generally, a graph G is represented as G = ( V , E )
where V is set of vertices
E is set of edges.
Example
The following is a graph with 5 vertices and 7 edges.
This graph G can be defined as G = ( V , E )
Where V = {A,B,C,D,E} and E = {(A,B),(A,C)(A,D),(B,D),(C,D),(B,E),(E,D)}.
Graph Terminology
Vertex
Individual data element of a graph is called as Vertex. Vertex is also known as node. In above example graph, A, B, C, D & E are known as vertices.
Edge
An edge is a connecting link between two vertices. Edge is also known as Arc. An edge is represented as (startingVertex, endingVertex).For example, in above graph the link between vertices A and B is represented as (A,B). In above example graph, there are 7 edges (i.e., (A,B), (A,C), (A,D), (B,D), (B,E), (C,D), (D,E)).
Edges are three types.
Undirected Edge - An undirected egde is a bidirectional edge. If there is undirected edge between vertices A and B then edge (A , B) is equal to edge (B , A).
Directed Edge - A directed egde is a unidirectional edge. If there is directed edge between vertices A and B then edge (A , B) is not equal to edge (B , A).
Weighted Edge - A weighted egde is a edge with value (cost) on it.
Degree
Total number of edges connected to a vertex is said to be degree of that vertex.
Total number of edges connected to a vertex is said to be degree of that vertex.
Indegree
Total number of incoming edges connected to a vertex is said to be indegree of that vertex.
Total number of incoming edges connected to a vertex is said to be indegree of that vertex.
Outdegree
Total number of outgoing edges connected to a vertex is said to be outdegree of that vertex.
Self-loop
Edge (undirected or directed) is a self-loop if its two endpoints coincide with each other.
Simple Graph
A graph is said to be simple if there are no parallel and self-loop edges.
Path
A path is a sequence of alternate vertices and edges that starts at a vertex and ends at other vertex such that each edge is incident to its predecessor and successor vertex.
Types of graphs
No comments:
Post a Comment